‘没有测量,就没有科学’这是科学家门捷列夫的名言。在计算机科学特别是机器学习领域中,对模型的评估同样至关重要,只有选择与问题相匹配的评估方法,才能快速地发现模型选择或训练过程中出现的问题,迭代地对模型进行优化。模型评估主要分为离线评估和在线评估两个阶段。针对分类、排序、回归、序列预测等不同类型的机器学习问题,评估指标的选择也有所不同。知道每种评估指标的精确定义、有针对性地选择合适的评估指标、更具评估指标的反馈进行模型调整,这些都是模型评估阶段的关键问题
评估指标
1. accuracy_score
分类准确率分数是指所有分类正确的百分比。分类准确率这一衡量分类器的标准比较容易理解,但是它不能告诉你响应值的潜在分布,并且它也不能告诉你分类器犯错的类型。
形式: sklearn.metrics.accuracy_score(y_true, y_pred, normalize=True, sample_weight=None)
normalize:默认值为True,返回正确分类的比例;如果为False,返回正确分类的样本数
示例:
1
2
3
4
5
6
7
8
>>>import numpy as np
>>>from sklearn.metrics import accuracy_score
>>>y_pred = [0, 2, 1, 3]
>>>y_true = [0, 1, 2, 3]
>>>accuracy_score(y_true, y_pred)
0.5
>>>accuracy_score(y_true, y_pred, normalize=False)
2
2. recall_score
召回率 =提取出的正确信息条数 /样本中的信息条数。通俗地说,就是所有准确的条目有多少被检索出来了。
形式: klearn.metrics.recall_score(y_true, y_pred, labels=None, pos_label=1,average=’binary’, sample_weight=None)
参数average : string, [None, ‘micro’, ‘macro’(default), ‘samples’, ‘weighted’]
将一个二分类matrics拓展到多分类或多标签问题时,我们可以将数据看成多个二分类问题的集合,每个类都是一个二分类。接着,我们可以通过跨多个分类计算每个二分类metrics得分的均值,这在一些情况下很有用。你可以使用average参数来指定。
macro:计算二分类metrics的均值,为每个类给出相同权重的分值。当小类很重要时会出问题,因为该macro-averging方法是对性能的平均。另一方面,该方法假设所有分类都是一样重要的,因此macro-averaging方法会对小类的性能影响很大。
weighted:对于不均衡数量的类来说,计算二分类metrics的平均,通过在每个类的score上进行加权实现。
micro:给出了每个样本类以及它对整个metrics的贡献的pair(sample-weight),而非对整个类的metrics求和,它会每个类的metrics上的权重及因子进行求和,来计算整个份额。Micro-averaging方法在多标签(multilabel)问题中设置,包含多分类,此时,大类将被忽略。
samples:应用在multilabel问题上。它不会计算每个类,相反,它会在评估数据中,通过计算真实类和预测类的差异的metrics,来求平均(sample_weight-weighted)
average:average=None将返回一个数组,它包含了每个类的得分. 示例:
1
2
3
4
5
6
7
8
9
10
11
>>>from sklearn.metrics import recall_score
>>>y_true = [0, 1, 2, 0, 1, 2]
>>>y_pred = [0, 2, 1, 0, 0, 1]
>>>recall_score(y_true, y_pred, average='macro')
0.33...
>>>recall_score(y_true, y_pred, average='micro')
0.33...
>>>recall_score(y_true, y_pred, average='weighted')
0.33...
>>>recall_score(y_true, y_pred, average=None)
array([1., 0., 0.])
3. f1_score
F1分数是精度和召回率的谐波平均值,正常的平均值平等对待所有的值,而谐波平均值回给予较低的值更高的权重,因此,只有当召回率和精度都很高时,分类器才能得到较高的F1分数。 其中,P代表Precision,R代表Recall。
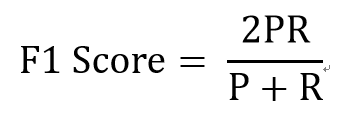
F1-Score指标综合了Precision与Recall的产出的结果。F1-Score的取值范围从0到1的,1代表模型的输出最好,0代表模型的输出结果最差。 示例:
1
2
3
4
5
>>>from sklearn.metrics import recall_score
>>>y_true = [0, 1, 2, 0, 1, 2]
>>>y_pred = [0, 2, 1, 0, 0, 1]
>>>f1_score(y_true, y_pred, average='macro')
0.57...
4. roc曲线
二值分类器是机器学习领域中最常见也是应用最广泛的分类器。评价二值分类器的指标很多,比如precision,recall,F1 score,P-R曲线等,但发现这些指标或多或少只能反映模型在某一方面的性能,相比而言,ROC曲线则有很多优点,经常作为评估二值分类器最重要的指标之一
ROC曲线是Receiver Operating Characteristic Curve的简称,中文名为’受试者工作特征曲线’
ROC曲线的横坐标为假阳性率(FPR),纵坐标为真阳性率(TPR),FPR和TPR的计算方法分别为:
𝐹𝑃𝑅=𝐹𝑃𝑁 𝑇𝑃𝑅=𝑇𝑃𝑃
P是真实的正样本数量,N是真实的负样本数量,TP是P个正样本中被分类器预测为正样本的个数,FP为N个负样本中被预测为正样本的个数。 示例:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
>>>import numpy as np
>>>from sklearn import metrics
>>>y = np.array([1, 1, 2, 2])
>>>scores = np.array([0.1, 0.4, 0.35, 0.8])
>>>fpr, tpr, thresholds = metrics.roc_curve(y, scores, pos_label=2)
>>>fpr
array([0. , 0.5, 0.5, 1. ])
>>>tpr
array([0.5, 0.5, 1. , 1. ])
>>>thresholds
array([0.8 , 0.4 , 0.35, 0.1 ])
>>>from sklearn.metrics import auc
>>>metrics.auc(fpr, tpr)
0.75
ROC曲线绘制
创建数据集
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
import pandas as pd
column_name = ['真实标签','模型输出概率']
datasets = [['p',0.9],['p',0.8],['n',0.7],['p',0.6],
['p',0.55],['p',0.54],['n',0.53],['n',0.52],
['p',0.51],['n',0.505],['p',0.4],['p',0.39],
['p',0.38],['n',0.37],['n',0.36],['n',0.35],
['p',0.34],['n',0.33],['p',0.30],['n',0.1]]
data = pd.DataFrame(datasets,index = [i for i in range(1,21,1)],columns=column_name)
print(data)
真实标签 模型输出概率
1 p 0.900
2 p 0.800
3 n 0.700
4 p 0.600
5 p 0.550
6 p 0.540
7 n 0.530
8 n 0.520
9 p 0.510
10 n 0.505
11 p 0.400
12 p 0.390
13 p 0.380
14 n 0.370
15 n 0.360
16 n 0.350
17 p 0.340
18 n 0.330
19 p 0.300
20 n 0.100
绘制ROC曲线
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# 计算各种概率情况下对应的(假阳率,真阳率)
points = {0.1:[1,1],0.3:[0.9,1],0.33:[0.9,0.9],0.34:[0.8,0.9],0.35:[0.8,0.8],
0.36:[0.7,0.8],0.37:[0.6,0.8],0.38:[0.5,0.8],0.39:[0.5,0.7],0.40:[0.4,0.7],
0.505:[0.4,0.6],0.51:[0.3,0.6],0.52:[0.3,0.5],0.53:[0.2,0.5],0.54:[0.1,0.5],
0.55:[0.1,0.4],0.6:[0.1,0.3],0.7:[0.1,0.2],0.8:[0,0.2],0.9:[0,0.1]}
X = []
Y = []
for value in points.values():
X.append(value[0])
Y.append(value[1])
import matplotlib.pyplot as plt
plt.scatter(X,Y,c = 'r',marker = 'o')
plt.plot(X,Y)
plt.xlim(0,1)
plt.ylim(0,1)
plt.xlabel('FPR')
plt.ylabel('TPR')
plt.show()
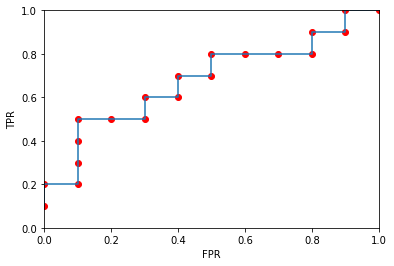
AUC指ROC曲线下的面积大小,该值能够量化地反映基于ROC曲线衡量出的模型性能,AUC越大说明分类器越可能把真正的正样本排在前面,分类性能越好
ROC曲线相比P-R曲线,当正负样本的分布发生变化时,ROC曲线的形状能够保存基本不变,而P-R曲线的形状一般会发生激烈的变化,这个特点让ROC曲线能够尽量降低不同测试集带来的干扰,更加客观地衡量模型本身的性能
5. Auc
计算AUC值,其中x,y分别为数组形式,根据(xi,yi)在坐标上的点,生成的曲线,然后计算AUC值;
形式: sklearn.metrics.auc(x, y, reorder=False)
6. roc_auc_score
直接根据真实值(必须是二值)、预测值(可以是0/1,也可以是proba值)计算出auc值,中间过程的roc计算省略。
形式: sklearn.metrics.roc_auc_score(y_true, y_score, average=’macro’, sample_weight=None)
average : string, [None, ‘micro’, ‘macro’(default), ‘samples’, ‘weighted’]
示例:
1
2
3
4
5
6
>>>import numpy as np
>>>from sklearn.metrics import roc_auc_score
>>>y_true = np.array([0, 0, 1, 1])
>>>y_scores = np.array([0.1, 0.4, 0.35, 0.8])
>>>roc_auc_score(y_true, y_scores)
0.75
7. confusion_matrix
用一个例子来理解混淆矩阵: 假设有一个用来对猫(cats)、狗(dogs)、兔子(rabbits)进行分类的系统,混淆矩阵就是为了进一步分析性能而对该算法测试结果做出的总结。假设总共有 27 只动物:8只猫, 6条狗, 13只兔子。结果的混淆矩阵如下图:
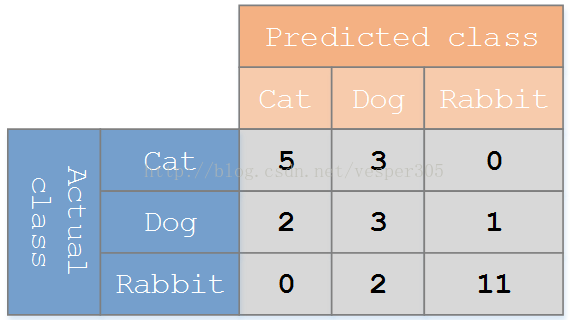
在这个混淆矩阵中,实际有 8只猫,但是系统将其中3只预测成了狗;对于 6条狗,其中有 1条被预测成了兔子,2条被预测成了猫。从混淆矩阵中我们可以看出系统对于区分猫和狗存在一些问题,但是区分兔子和其他动物的效果还是不错的。所有正确的预测结果都在对角线上,所以从混淆矩阵中可以很方便直观的看出哪里有错误,因为他们呈现在对角线外面。
评估方法
1. 使用numpy计算
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
import numpy as np
y_true = np.array([0, 1, 1, 0, 1, 0])
y_pred = np.array([1, 1, 1, 0, 0, 1])
# true positive
TP = np.sum(np.multiply(y_true, y_pred))
print(TP)
# false positive
FP = np.sum(np.logical_and(np.equal(y_true, 0), np.equal(y_pred, 1)))
print(FP)
# false negative
FN = np.sum(np.logical_and(np.equal(y_true, 1), np.equal(y_pred, 0)))
print(FN)
# true negative
TN = np.sum(np.logical_and(np.equal(y_true, 0), np.equal(y_pred, 0)))
print(TN)
输出结果:
1
2
3
4
2
2
1
1
2. 使用tensorflow计算
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
import tensorflow as tf
sess = tf.Session()
y_true = tf.constant([0, 1, 1, 0, 1, 0])
y_pred = tf.constant([1, 1, 1, 0, 0, 1])
# true positive
TP = tf.reduce_sum(tf.multiply(y_true, y_pred))
print(sess.run(TP))
# false positive
FP = tf.reduce_sum(tf.cast(tf.logical_and(tf.equal(y_true, 0), tf.equal(y_pred, 1)), tf.int32))
print(sess.run(FP))
# false negative
FN = tf.reduce_sum(tf.cast(tf.logical_and(tf.equal(y_true, 1), tf.equal(y_pred, 0)), tf.int32))
print(sess.run(FN))
# true negative
TN = tf.reduce_sum(tf.cast(tf.logical_and(tf.equal(y_true, 0), tf.equal(y_pred, 0)), tf.int32))
print(sess.run(TN))
输出结果:
1
2
3
4
2
2
1
1
3. 使用sklearn的metrics模块计算
3.1 数据是list类型
1
2
3
4
5
6
7
8
9
10
11
12
from sklearn.metrics import precision_score, recall_score, f1_score
y_true = [0, 1, 1, 0, 1, 0]
y_pred = [1, 1, 1, 0, 0, 1]
p = precision_score(y_true, y_pred, average='binary')
r = recall_score(y_true, y_pred, average='binary')
f1score = f1_score(y_true, y_pred, average='binary')
print(p)
print(r)
print(f1score)
输出结果:
1
2
3
0.5
0.666666666667
0.571428571429
3.2 数据是ndarray类型
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from sklearn.metrics import precision_score, recall_score, f1_score
import numpy as np
y_true = np.array([[0, 1, 1],
[0, 1, 0]])
y_pred = np.array([[1, 1, 1],
[0, 0, 1]])
y_true = np.reshape(y_true, [-1])
y_pred = np.reshape(y_pred, [-1])
p = precision_score(y_true, y_pred, average='binary')
r = recall_score(y_true, y_pred, average='binary')
f1score = f1_score(y_true, y_pred, average='binary')
print(p)
print(r)
print(f1score)
输出结果:
1
2
3
0.5
0.666666666667
0.571428571429