混淆矩阵(confusion matrix)
混淆矩阵也称误差矩阵,是表示精度评价的一种标准格式,用n行n列的矩阵形式来表示。具体评价指标有总体精度、制图精度、用户精度等,这些精度指标从不同的侧面反映了图像分类的精度。在人工智能中,混淆矩阵(confusion matrix)是可视化工具,特别用于监督学习,在无监督学习一般叫做匹配矩阵。矩阵的每一行表示预测类中的实例,而每一列表示实际类中的实例(反之亦然)。 这个名字源于这样一个事实,即很容易看出系统是否混淆了两个类。
一句话解释版本:
混淆矩阵就是分别统计分类模型归错类,归对类的观测值个数,然后把结果放在一个表里展示出来。这个表就是混淆矩阵。
下图是混淆矩阵的一个例子

其中灰色部分是真实分类和预测分类结果相一致的,绿色部分是真实分类和预测分类不一致的,即分类错误的。
二分类用例
以分类模型中最简单的二分类为例,对于这种问题,我们的模型最终需要判断样本的结果是0还是1,或者说是positive还是negative。
我们通过样本的采集,能够直接知道真实情况下,哪些数据结果是positive,哪些结果是negative。同时,我们通过用样本数据跑出分类型模型的结果,也可以知道模型认为这些数据哪些是positive,哪些是negative。
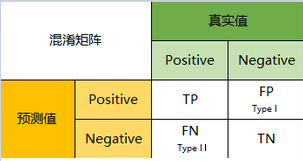
因此,我们就能得到这样四个基础指标,我称他们是一级指标(最底层的):
1
2
3
4
真实值是positive,模型认为是positive的数量(True Positive=TP)
真实值是positive,模型认为是negative的数量(False Negative=FN):这就是统计学上的第二类错误(Type II Error)
真实值是negative,模型认为是positive的数量(False Positive=FP):这就是统计学上的第一类错误(Type I Error)
真实值是negative,模型认为是negative的数量(True Negative=TN)
将这四个指标一起呈现在表格中,就能得到如下这样一个矩阵,我们称它为混淆矩阵(Confusion Matrix):
混淆矩阵的指标
预测性分类模型,肯定是希望越准越好。那么,对应到混淆矩阵中,那肯定是希望TP与TN的数量大,而FP与FN的数量小。所以当我们得到了模型的混淆矩阵后,就需要去看有多少观测值在第二、四象限对应的位置,这里的数值越多越好;反之,在第一、三象限对应位置出现的观测值肯定是越少越好。
二级指标
但是,混淆矩阵里面统计的是个数,有时候面对大量的数据,光凭算个数,很难衡量模型的优劣。因此混淆矩阵在基本的统计结果上又延伸了如下4个指标,我称他们是二级指标(通过最底层指标加减乘除得到的):
1
2
3
4
准确率(Accuracy)针对整个模型
精确率(Precision)
灵敏度(Sensitivity):就是召回率(Recall)
特异度(Specificity)
用表格的方式将这四种指标的定义、计算、理解进行了汇总:
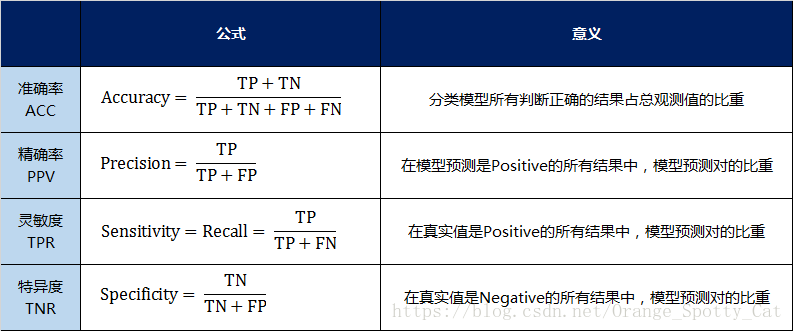
通过上面的四个二级指标,可以将混淆矩阵中数量的结果转化为0-1之间的比率。便于进行标准化的衡量。
在这四个指标的基础上在进行拓展,会产令另外一个三级指标。
三级指标
这个指标叫做F1 Score。他的计算公式是:
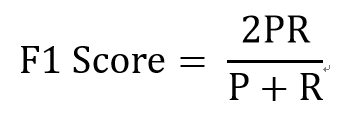
其中,P代表Precision,R代表Recall。
F1-Score指标综合了Precision与Recall的产出的结果。F1-Score的取值范围从0到1的,1代表模型的输出最好,0代表模型的输出结果最差。
混淆矩阵的实例
当分类问题是二分问题是,混淆矩阵可以用上面的方法计算。当分类的结果多于两种的时候,混淆矩阵同时适用。
以下面的混淆矩阵为例,我们的模型目的是为了预测样本是什么动物,这是我们的结果:
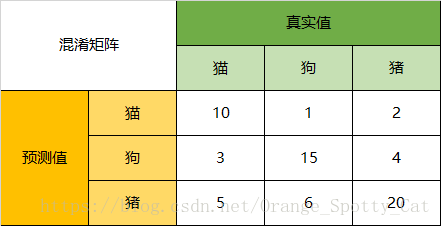
通过混淆矩阵,我们可以得到如下结论:
Accuracy
在总共66个动物中,我们一共预测对了10 + 15 + 20=45个样本,所以准确率(Accuracy)=45/66 = 68.2%。
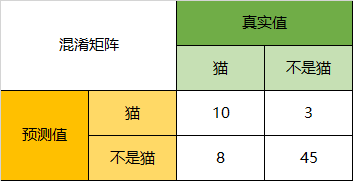
以猫为例,我们可以将上面的图合并为二分问题:
Precision
所以,以猫为例,模型的结果告诉我们,66只动物里有13只是猫,但是其实这13只猫只有10只预测对了。模型认为是猫的13只动物里,有1条狗,两只猪。所以,Precision(猫)= 10/13 = 76.9%
Recall
以猫为例,在总共18只真猫中,我们的模型认为里面只有10只是猫,剩下的3只是狗,5只都是猪。这5只八成是橘猫,能理解。所以,Recall(猫)= 10/18 = 55.6%
Specificity
以猫为例,在总共48只不是猫的动物中,模型认为有45只不是猫。所以,Specificity(猫)= 45/48 = 93.8%。
虽然在45只动物里,模型依然认为错判了6只狗与4只猫,但是从猫的角度而言,模型的判断是没有错的。(这里是参见了Wikipedia,Confusion Matrix的解释,https://en.wikipedia.org/wiki/Confusion_matrix)
F1-Score
通过公式,可以计算出,对猫而言,F1-Score=(2 * 0.769 * 0.556)/( 0.769 + 0.556) = 64.54%
同样,我们也可以分别计算猪与狗各自的二级指标与三级指标值。
方法调用
官方文档中给出的用法是
1
2
3
4
5
sklearn.metrics.confusion_matrix(y_true, y_pred, labels=None, sample_weight=None)
y_true: 是样本真实分类结果,
y_pred: 是样本预测分类结果
labels:是所给出的类别,通过这个可对类别进行选择
sample_weight : 样本权重
实现例子:
1
2
3
4
5
6
from sklearn.metrics import confusion_matrix
y_true=[2,1,0,1,2,0]
y_pred=[2,0,0,1,2,1]
C=confusion_matrix(y_true, y_pred)
运行结果:
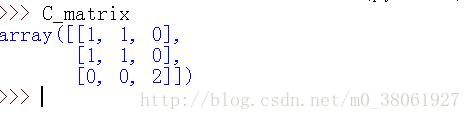
这儿没有标注类别:下图是标注类别以后,更加好理解

绘制混淆矩阵
混淆矩阵的计算
混淆矩阵就是我们会计算最后分类错误的个数, 如计算将class1分为class2的个数,以此类推。
我们可以使用下面的方式来进行混淆矩阵的计算。
1
2
3
4
5
6
7
8
9
10
# 绘制混淆矩阵
def confusion_matrix(preds, labels, conf_matrix):
preds = torch.argmax(preds, 1)
for p, t in zip(preds, labels):
conf_matrix[p, t] += 1
return conf_matrix
conf_matrix = torch.zeros(10, 10)
for data, target in test_loader:
output = fullModel(data.to(device))
conf_matrix = confusion_matrix(output, target, conf_matrix)
最后得到的conf_matrix就是混淆矩阵的值。
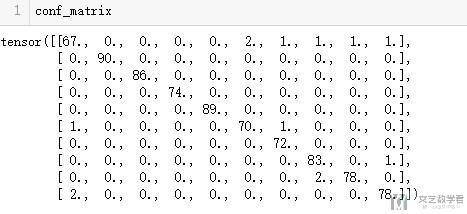
混淆矩阵的绘制(Plot a confusion matrix)
有了上面的混淆矩阵中具体的值,下面就是进行可视化的步骤。可视化我们使用seaborn来进行完成。因为我这里conf_matrix的值是tensor, 所以需要先转换为Numpy.
1
2
3
4
5
6
import seaborn as sn
df_cm = pd.DataFrame(conf_matrix.numpy(),
index = [i for i in list(Attack2Index.keys())],
columns = [i for i in list(Attack2Index.keys())])
plt.figure(figsize = (10,7))
sn.heatmap(df_cm, annot=True, cmap="BuPu")
最终的混淆矩阵的图如下所示:
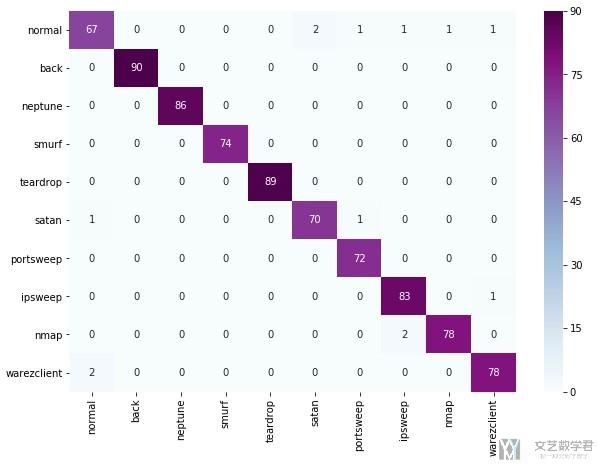
混淆矩阵的可视化(进行美化)
我们还可以对混淆矩阵做更多的处理, 使得显示的时候能更加好看一些. 下面的绘制混淆矩阵的函数我是在下面的链接里看到的, 最终的效果很是不错。
参考链接 : AE_RL_NSL_KDD
这里简单贴一下代码,可以方便直接进行使用。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
import itertools
# 绘制混淆矩阵
def plot_confusion_matrix(cm, classes, normalize=False, title='Confusion matrix', cmap=plt.cm.Blues):
"""
This function prints and plots the confusion matrix.
Normalization can be applied by setting `normalize=True`.
Input
- cm : 计算出的混淆矩阵的值
- classes : 混淆矩阵中每一行每一列对应的列
- normalize : True:显示百分比, False:显示个数
"""
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
print("Normalized confusion matrix")
else:
print('Confusion matrix, without normalization')
print(cm)
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
fmt = '.2f' if normalize else 'd'
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, format(cm[i, j], fmt),
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
测试数据如下所示:
1
2
3
4
5
6
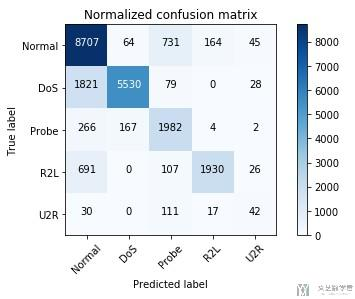
cnf_matrix = np.array([[8707, 64, 731, 164, 45],
[1821, 5530, 79, 0, 28],
[266, 167, 1982, 4, 2],
[691, 0, 107, 1930, 26],
[30, 0, 111, 17, 42]])
attack_types = ['Normal', 'DoS', 'Probe', 'R2L', 'U2R']
我们分别测试normalize=True/False的效果。
1
plot_confusion_matrix(cnf_matrix, classes=attack_types, normalize=True, title='Normalized confusion matrix')
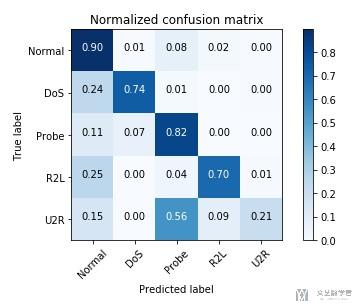
1
plot_confusion_matrix(cnf_matrix, classes=attack_types, normalize=False, title='Normalized confusion matrix')